Array Operations – Engineering and Technology Blogger

Table of Contents show

Numpy Operations

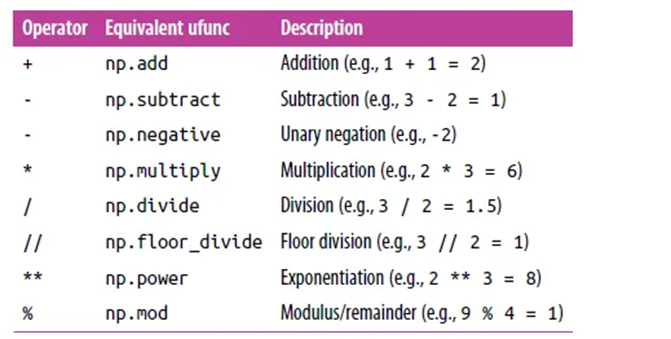
Arithmetic functions

Arithmetic operators on arrays apply elementwise. A new array is created and filled with the result

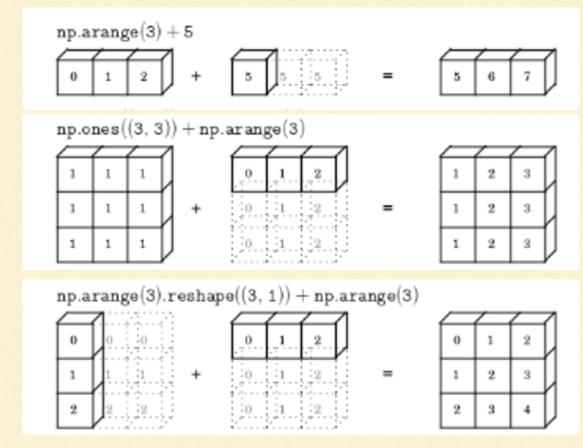
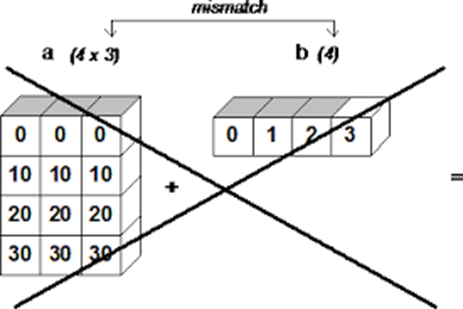
Broadcasting Rules

Two arrays are compatible for broadcasting if for each trailing dimension ( that is starting from the end), the axis lengths match or if either of the lengths is 1. Broadcasting is then performed over the missing and / or length 1 dimensions

Addition

a1 = [[0. 1. 2.][3. 4. 5.][6. 7. 8.]]
a2 = [10 10 10]
c1 = np.add(a1,a2) #a1 + a2
print("Result of Add	ition=",c1)
print("\n")

Result of Addition = [[10. 11. 12.][13. 14. 15.][16. 17. 18.]]

Subtraction

a1 = [[0. 1. 2.][3. 4. 5.][6. 7. 8.]]
a2 = [10 10 10]
c2 = np.subtract(a1,a2) #a1 - a2
print("Result of subtraction=",c2)
print("\n")

Result of Subtraction= [[-10. -9. -8.][-7. -6. -5.][-4. -3. -2.]]

Multiplication

a1 = [[0. 1. 2.][3. 4. 5.][6. 7. 8.]]
a2 = [10 10 10]
c3 = np.multiply(a1,a2) #a1 - a2
print("Result of multiplication=",c3)
print("\n")

Result of Multiplication = [[0. 10. 20.][30. 40. 50.][60. 70. 80.]]

Division

a1 = [[0. 1. 2.][3. 4. 5.][6. 7. 8.]]
a2 = [10 10 10]
c4 = np.divide(a1,a2) #a1 - a2
print("Result of division=",c4)
print("\n")

Result of Division= [[0. 0.1 0.2][0.3 0.4 0.5][0.6 0.7 0.8]]

Reciprocal

Reciprocal: calculates : 1/x

note: np.reciprocal is not working for integers

#Reciprocal
a3 = np.array([4,0.25,0.01,-0.25, 0])
a4 = np.reciprocal(a3)
print("Result of reciprocal=",a4)
print("\n")
a5 = np.array([100]) 
print("Reciprocal of integer = ",np.reciprocal(a5))
print("\n")

Power

Elements in the first input array is base and returns it raised to the power of the corresponding element in the second input array

base = np.array( [10,20,30] )
print("Calculating power(array, scalar)= ",np.power(base,2))
print("\n")
root = np.array( [2,3,4] )
print("Calculating power(array, array)= ",np.power(base,root))
print("\n")

Calculating power(array, scalar) = [100 400 900]
Calculating power(array, array) = [   100   8000 810000]

Modulus

Returns the remainder of division of the corresponding elements in the input array

numpy.mod() is similar to numpy.remainder( )

dividend = np.array( [100.0, 40, 33] )
divisor = np.array ([2,3,6])
print("Calculating mod using mod() = ", np.mod(dividend, divisor))
print("Calculating mod using remainder() = ", np.remainder(dividend, divisor))
print("\n")

Calculating mod using mod() = [0. 1. 3.]
Calculating mod using remainder() = [0. 1. 3.]

Function for working on complex numbers,

numpy.real() – returns the real part of the complex data type argument

numpy.image() – returns the imaginary part of the complex data type argument

numpy.cong() – returns the complex conjugate, which is obtained by changing the sign of the imaginary part

numpy.angle() – returns the angle of the complex argument. The function has degree parameter. If true the angle in the degree is returned. Otherwise, the angle in radians

numpy.angle : works as if z = x+iy; then it computes taninverse of (y/x) in radians as well as in angle

c1 = np.array( [-4.3j,1+1.2j, 10, -10-10j] )
print("c1=",c1)
print("\n")
print("Real numbers in c1", np.real(c1))
print("Imaginary numbers in c1", np.imag(c1))
print("Conjugate in c1", np.conj(c1))
print("Angle in radians:", np.angle (c1))
print("Angle in degrees:",np.angle(c1,deg=True))

Real numbers in c1 [ -0.   1.  10. -10.]
Imaginary numbers in c1 [ -4.3   1.2   0.  -10. ]
Conjugate in c1 [ -0. +4.3j   1. -1.2j  10. -0.j  -10.+10.j ]
Angle in radians: [-1.57079633  0.87605805  0.         -2.35619449]
Angle in degrees: [ -90.           50.19442891    0.         -135.        ]
<ipython-input-2-b0fbbecd7093>:33: RuntimeWarning: divide by zero encountered in reciprocal
  a4 = np.reciprocal(a3)

Statistical Functions

np.amin() : determines the minimum value of the element along a specified axis

np.amax() : determines the maximum value of the element along a specified axis

np.mean( ): determines the mean value of the data set

np.median( ): determines the median value of the data set

np.std( ): determines the standard deviation

np.var : determines the variance

np.ptp( ): returns a range of values along an axis

np.average(): determines the weighted average

np.percentile(): determines the nth percentile of data along the specified axis

sf = np.array( [[4,5,1],[10,0,20],[2,4,3]])
print("The array",sf)

The array [[ 4  5  1]
 [10  0 20]
 [ 2  4  3]]

np.amin

Return the minimum element of an array or minimum element along the axis

Syntax

np.amin(a,axis)

a: indicates input data in the form of an array

axis: optional parameter indicating the acis or axes along which to operate

Returns

The minimum value of any given array
If the axis is none, the result will be a scalar value
If the axis is given, the result is an array of dimension a.ndim-1

When axis value is not passed to min() function, then it returns the minimum element present in the array

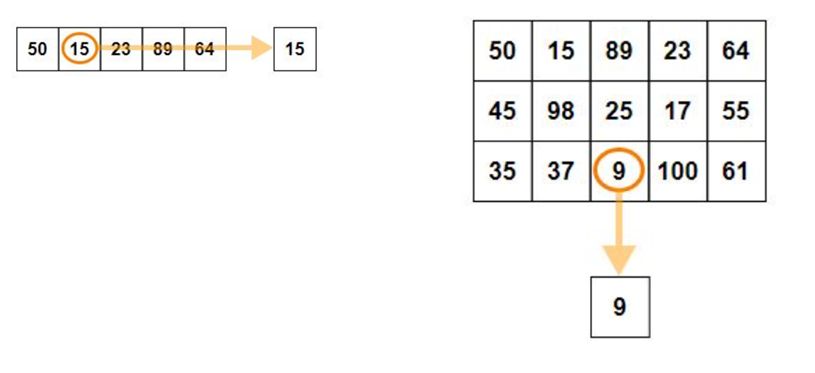
Min value in each column when axis = 0

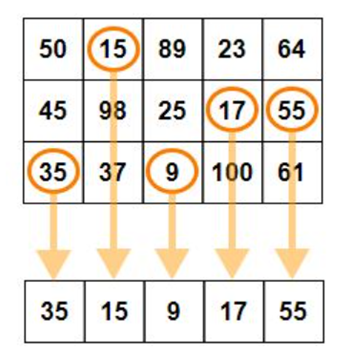
Min value in each row when axis = 1

Finding Minimum

print("The minimum element in array:", np.amin(sf))
print("The minimum element in array along axis 0:", np.amin(sf, axis=0))
print("The minimum element in array along axis 1:", np.amin(sf, axis=1))

The minimum element in array: 0
The minimum element in array along axis 0: [2 0 1]
The minimum element in array along axis 1: [1 0 2]

np.amax

To get a maximum value along the a specified axis

Syntax

np.amax(a,axis=None)

a: parameter refers to the array on which you want to apply np.max() function

axis parameter is optional and helps us to specify the axis on which we want to find the maximum values

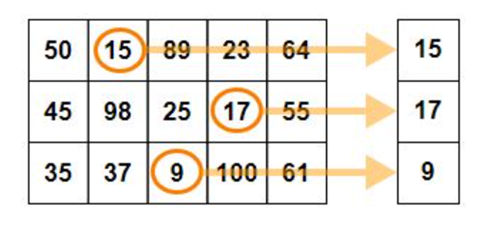
When axis value is not passed to max() function, then it returns the maximum element present in the array-

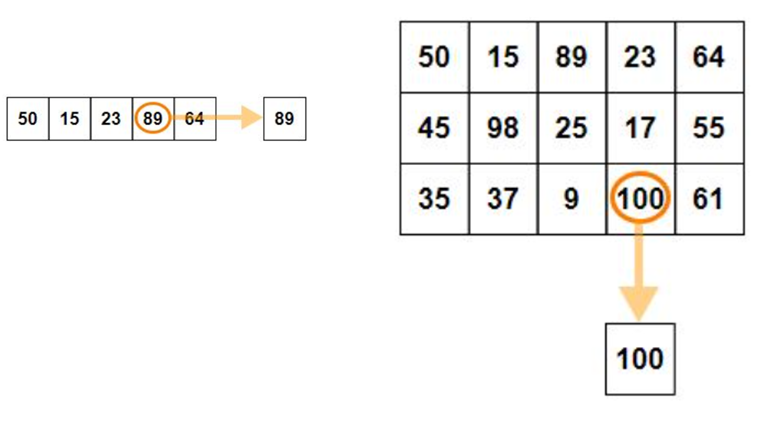
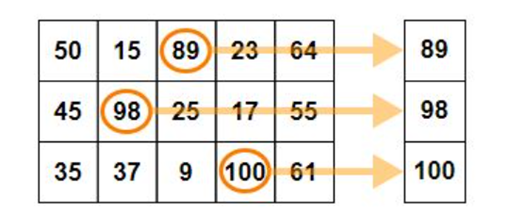
Max value in each column when axis = 0

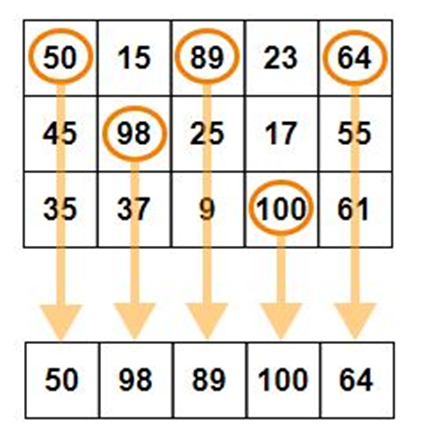
Max value in each row when axis = 1

Finding Maximum

#Finding Maximum
print("The maximum element in array:", np.amax(sf))
print("The maximum element in array along axis 0:",np.amax(sf, axis=0))
print("The maximum element in array along axis 1:",np.amax(sf,axis= 1))

The maximum element in array: 20
The maximum element in array along axis 0: [10  5 20]
The maximum element in array along axis 1: [ 5 20  4]

np.mean

Statistic measure for summarizing data is the average or mean
Mean is caculated by summing all the values and divided by the count of values

\[\overline{x} = \frac{\sum_{i=1}^{n} x_i}{n}\]

Example: [0,1,1,2,9]

Mean = [0+1+1+2+9] /5 = 2.6

Sensitive to outliers

9 is very larger than other numbers and thus pull the mean higher

Syntax

np.mean(a,axis=None)

a: an array

axis: parameter is optional and is used to specify the axis along which to compute mean

When no axis is passed, then arithmetic mean is computed for entire array

When no value for axis is specified

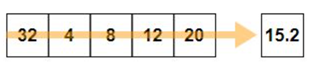
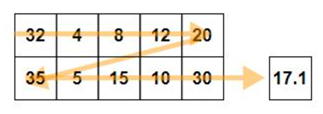
axis = 0 is passed to mean

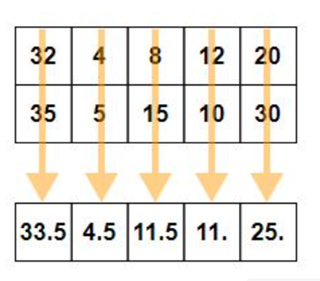
axis = 1 is passed to mean

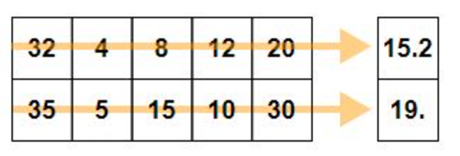
print("Mean of array:",np.mean(sf))
print("Mean of array along axis 0:",np.mean(sf,axis = 0))
print("Mean of array along axis 1:",np.mean(sf,axis = 1))

Mean of array: 5.444444444444445
Mean of array along axis 0: [5.33333333 3.         8.        ]
Mean of array along axis 1: [ 3.33333333 10.          3.        ]

np.median

When there are outliers in the data, median can be used
Median – measure of central tendency
Robust to outliers

Median represents 50^th percentile of the data

i.e. 50% of the values are greater than the median
50% of the values are less than the median
ODD numbers: (n+1)/2
Even number: average of values present in index – (n/2) and (n/2) +1

print("Median of array:",np.median(sf))
print("Median of array along axis 0:",np.median(sf,axis=0))
print("Median of array along axis 1:",np.median(sf,axis=1))

print("Median of array:",np.median(sf))
print("Median of array along axis 0:",np.median(sf,axis=0))
print("Median of array along axis 1:",np.median(sf,axis=1))

numpy.ptp

numpy.ptp stands for peak to peak
Use to return a range of values along an axis
Range is calculated as maximum value – minimum value

Syntax

numpy.ptp( a, axis = none)

a – input to indicate array

axis – used to indicate the axis along in which to compute range. Default: input array is flattened by taking all the numbers; axis = 0 means along the column; and axis = 1 means working along the row

Returns

A scalar value ( if axis is none) else return an range of values
When the data is having outliers, range is rendered useless.
Range does not tell how the data is dispersed; rather it tells how dispersed entire dataset is

print("range = ", np.ptp(sf))
print("range along (axis = 0)  is= ", np.ptp(sf,axis=0))
print("range along (axis = 1)  is= ", np.ptp(sf,axis=1))

range =  20
range along (axis = 0)  is=  [ 8  5 19]
range along (axis = 1)  is=  [ 4 20  2]

np.var

Describes, how far apart observations are spread out from their average value

Formula

\[{s^2} = \frac{\sum_{i=1}^{n}{(x_i – \overline{x})}^2}{n}\]

Syntax

np.var(a,axis)

a: represents input array

axis: represents the axis along which we want to compute standard deviation

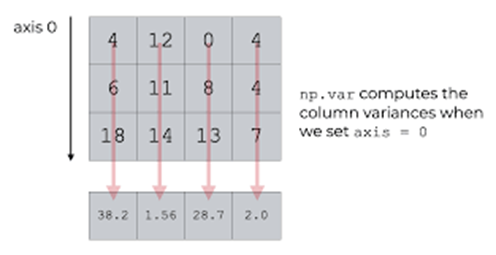
axis = 0 // along the column
axis = 1 // along the row

print("variance of array:",np.var(sf))
print("variance of array along axis 0:",np.var(sf,axis=0))
print("variance of array along axis 1:",np.var(sf,axis=1))

variance of array: 33.80246913580247
variance of array along axis 0: [11.55555556  4.66666667 72.66666667]
variance of array along axis 1: [ 2.88888889 66.66666667  0.66666667]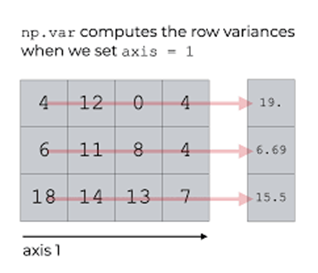

np.std

Standard deviation – square root of the variance

\[s = \sqrt{\frac{\sum_{i=1}^{n}{(x_i – \overline{x})}^2}{n}}\]

Standard deviation inference

Small standard deviation means that values are close to the mean Large standard deviation means that values are dispersed more widely

Syntax

np.std(a,axis)

a: represents input array

axis: represents the axis along which we want to compute standard deviation

axis = 0 // along the column
axis = 1 // along the row

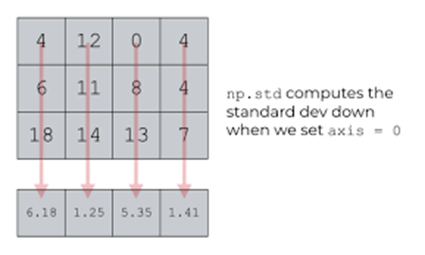
print("SD of array:",np.std(sf))
print("SD of array along axis 0:",np.std(sf,axis=0))
print("SD of array along axis 1:",np.std(sf,axis=1))

SD of array: 5.813989089756057
SD of array along axis 0: [3.39934634 2.1602469  8.52447457]
SD of array along axis 1: [1.69967317 8.16496581 0.81649658]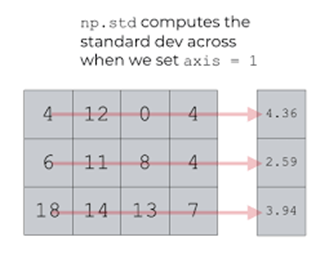

np.percentile

Percentile and quartiles are both quantiles: values that divide data into equal groups each containing the same percentage of the total data. Percentiles gives this in 100 parts.

The q-th percentile gives a value below which q percentage of the values fall.
For example, the 10th percentile gives a value below which 10% of the values fall.

numpy.percentile(a, q, axis=None, interpolation=None)

a: array
q: quantile
axis: along the column, axis = 0; along the row axis = 1
interpolation

interpolation : {‘linear’, ‘lower’, ‘higher’, ‘midpoint’, ‘nearest’}

This optional parameter specifies the interpolation method to use, when the desired quantile lies between two data points i and j:

linear: i + (j – i) * fraction, where fraction is the fractional part of the index surrounded by i and j.
lower: i.
higher: j.
nearest: i or j whichever is nearest.
midpoint: (i + j) / 2.

If  q = 50, then the function is same as median
If q = 0, then the function is same as minimum 
If q = 100, then the function is same as maximum
aw = np.array([2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325])
calculate r = q * (n / 100) 
r = 85*(12/100) = 10.2
highest - next index of 10.2 i.e element at index 11
lowest - integer index less than 10.2 i.e. element at index 10
linear - (i+(j-i)*fraction) = 3050 +(3130-3050)*0.2= 3066
nearest - the nearest index for 10.2 is 10. so element at index 10 
midpoint - (i+j)/2 = (3050 + 3130)/2 = 3090

aw = np.array([2710,2755,2850,2880,2880,2890,2920,2940,2950,3050,3130,3325])
print("interpolation = higher",np.percentile(aw,85,interpolation='higher'))
print("interpolation = lower",np.percentile(aw,85,interpolation='lower'))
print("interpolation = linear",np.percentile(aw,100,interpolation='linear'))
print("interpolation = nearest",np.percentile(aw,85,interpolation='nearest'))
print("interpolation = midpoint",np.percentile(aw,85,interpolation='midpoint'))

interpolation = higher 3130
interpolation = lower 3050
interpolation = linear 3325.0
interpolation = nearest 3050
interpolation = midpoint 3090.0

Bitwise Operators

Bitwise And Operator

np.bitwise_and

Performs bitwise AND on two array elements

Sets each bit to 1 if both bits are 1

#bitwise_and
ba = 10
bb = 15
print("binary of",ba,":",bin(ba))
print("binary of",bb,":",bin(bb))
result = np.bitwise_and(ba,bb)
print("Result of bitwise_and=",result)

binary of 10 : 0b1010
binary of 15 : 0b1111
Result of bitwise_and= 10

np.bitwise_or

Performs bitwise or on two array elements

Sets each bit to 1 if one of two bits is 1

#bitwise_or
ba = 10
bb = 15
print("binary of",ba,":",bin(ba))
print("binary of",bb,":",bin(bb))
result1 = np.bitwise_or(ba,bb)
print("Result of bitwise_or=",result1)

binary of 10 : 0b1010
binary of 15 : 0b1111

Result of bitwise_or= 15

np.bitwise_and and np.bitwise_or

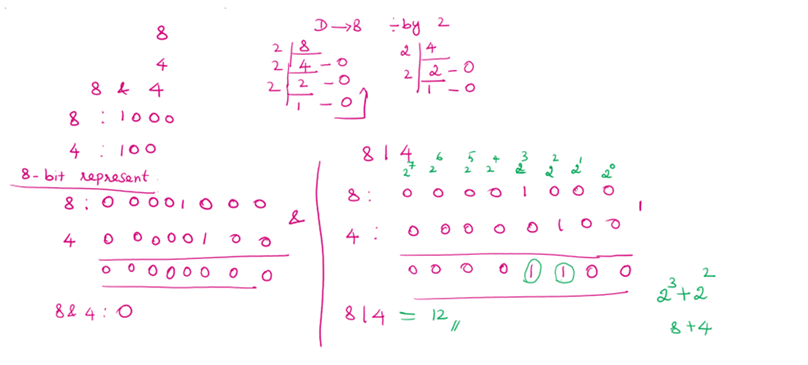
np.bitwise_invert()

Invert all the bits

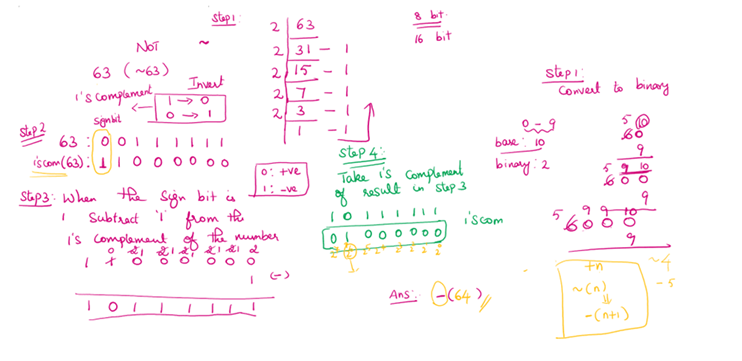
np.invert()

#invert
result2 = np.invert(ba)
print("bitwise_invert(",ba,")=",result2)

bitwise_invert( 10 )= -11

np.bitwise_xor

Performs bitwise XOR on two array elements

Sets each bit to 1 if only one of two bits is 1

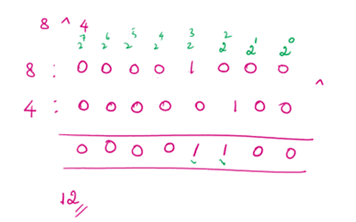
result3 = np.bitwise_xor(ba,bb)
print("bitwise_xor(",ba,bb,")=",result3)

bitwise_xor( 10 15 )= 5

np.left_shift

Left shift operator shifts binary representation of array elements towards the left
Takes two parameters: array, number of positions to shift
The array shift towards left by appending zeros to its right

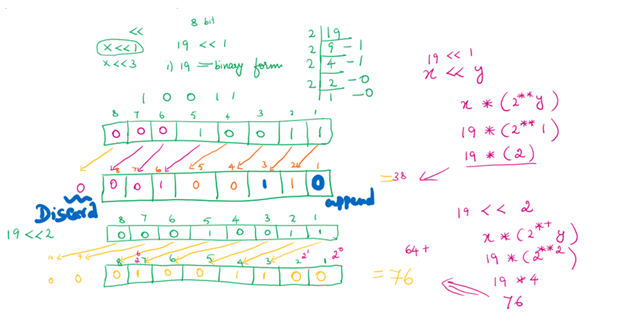
#bitwise_leftshift
result4 = np.left_shift(ba,2)
print("left_shift(",ba,2,")=",result4)

left_shift( 10 2 )= 40

np.right_shift()

Right shift operator shifts binary representation of array elements towards theright
Takes two parameters: array, number of positions to shift
The array shift towards right by appending zeros to its left

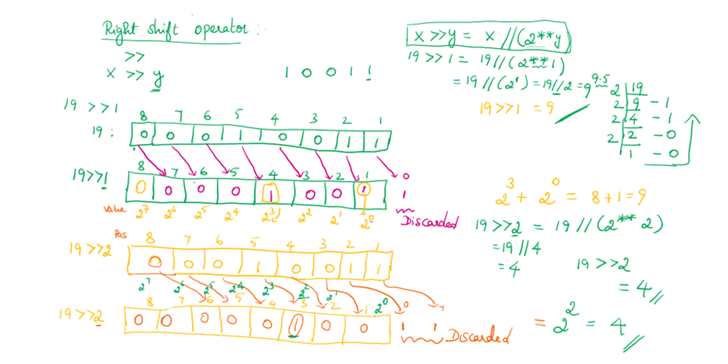
#bitwise_rightshift
result5 = np.right_shift(ba,2)
print("right_shift(",ba,2,")=",result5)

right_shift( 10 2 )= 2

Copying and Viewing Array

When operating and manipulating arrays, their data is sometimes copies into a new array and sometimes not

There are three cases,

No Copy at All
View or Shallow Copy
Deep Copy

No Copy at All

Simple assignments make no copy of array objects or of their data
The assignment operator does not create a copy of array. It actually accesses the original array through its id()

#No Copy at All
#Declare an array
arr1 = np.arange(10)
print("array =",arr1)
print("ID of arr1=",id(arr1))
#assign arr2
arr2 = arr1
print("arr2 has:",arr2)
print("ID of arr2=",id(arr2))
#change value of arr1[0]
arr1[0]= 100
print("After changing: arr1 =",arr1)
print("After changing: arr2 =",arr2)
arr2[3] =150
print("Now changing: arr1 =",arr1)
print("Now changing: arr2 =",arr2)

array = [0 1 2 3 4 5 6 7 8 9]
ID of arr1= 2327220408368
arr2 has: [0 1 2 3 4 5 6 7 8 9]
ID of arr2= 2327220408368
After changing: arr1 = [100   1   2   3   4   5   6   7   8   9]
After changing: arr2 = [100   1   2   3   4   5   6   7   8   9]
Now changing: arr1 = [100   1   2 150   4   5   6   7   8   9]
Now changing: arr2 = [100   1   2 150   4   5   6   7   8   9]

#No Copy at all
arr3 = np.arange(12)
arr4 = arr3 # no new object is created
print("arr4 is arr3",arr4 is arr3)
print("shape of arr3:",arr3.shape)
print("shape of arr4:",arr4.shape)
print("Before,arr 3=",arr3)
print("Before,arr 4=",arr4)
arr4.shape = (4,3)
print("Now,shape of arr3:",arr3.shape)
print("Now,shape of arr4:",arr4.shape)
print("After,arr 3=",arr3)
print("After,arr 4=",arr4)

arr4 is arr3 True
shape of arr3: (12,)
shape of arr4: (12,)
Before,arr 3= [ 0  1  2  3  4  5  6  7  8  9 10 11]
Before,arr 4= [ 0  1  2  3  4  5  6  7  8  9 10 11]
Now,shape of arr3: (4, 3)
Now,shape of arr4: (4, 3)
After,arr 3= [[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]
After,arr 4= [[ 0  1  2]
 [ 3  4  5]
 [ 6  7  8]
 [ 9 10 11]]

Python passes mutable objects as references. so function call does not make copy

def fun(x):
    print("Inside function",id(x))

arr5 = np.arange(5)
print("Outside function:",id(arr5))
fun(arr5)

Outside function: 2327220551808
Inside function 2327220551808

View or shallow copy

It returns a view of the original array stored at the existing location
The view does not have its own data or memory but uses the original array
The modification reflect in both
The view function is called as shallow copy

Different array objects can share the same data. The view method creates a new array object that looks at the same data

Slicing an array return a view of it

arr6 = np.arange(12)
arr7 = arr6.view()
print("arr7 is arr6=",arr7 is arr6)
print("arr6 is base for arr7=",arr7.base is arr6)
print("whetehr arr7 owns data=",arr7.flags.owndata)
#change the shape of arr7
arr7.shape=(4,3)
print("shape of arr6=",arr6.shape) #arr6 shape does not change
#change the value
arr7[1,2] = 100 # also changes value in arr6
print("arr6=",arr6)
print("id(arr6)",id(arr6))
print("id(arr7)",id(arr7))

arr7 is arr6= False
arr6 is base for arr7= True
whetehr arr7 owns data= False
shape of arr6= (12,)
arr6= [  0   1   2   3   4 100   6   7   8   9  10  11]
id(arr6) 2327220357440
id(arr7) 2327220356160

flags- Information about the memory layout of the array

Owndata – the array owns the memory it uses or borrows it from another object

#slicing an array returns a view of it
arr8 = np.arange(12).reshape(3,4)
print("arr8 =",arr8)
arr9 = arr8[:,1:3]
print("arr9=",arr9)
arr9[:] = 10 #If any changes made in view, changes data in original array also
print("Changes in view, changes original array,arr8=",arr8)
arr8[0,2] = 10000 #if any changes made in original array, changes view also
print("Changes in original array,changes view",arr9)

arr8 = [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]]
arr9= [[ 1  2]
 [ 5  6]
 [ 9 10]]
Changes in view, changes original array,arr8= [[ 0 10 10  3]
 [ 4 10 10  7]
 [ 8 10 10 11]]
Changes in original array,changes view [[   10 10000]
 [   10    10]
 [   10    10]]

Deep Copy

The copy method makes a complete copy of the array and its data
It returns a copy of the original array stored at a new location
The copy does not share data or memory with the original array
The modifications are not reflected.

arr10 = np.arange(10)
arr11 = arr10.copy()
print("arr11 is arr10 =",arr11 is arr10)
print("whether arr10 is base for arr11=",arr11.base is arr10)
#change the value in copied array
arr11[0] = 10000 #does not change in original array
print("Original array",arr10)

arr11 is arr10 = False
whether arr10 is base for arr11= False
Original array [0 1 2 3 4 5 6 7 8 9]

arr12 = np.arange(20).reshape(5,4)
arr13 = arr12[:,:2].copy()
print("arr12=",arr12)
print("arr13=",arr13)
print("id(arr12)=",id(arr12))
print("id(arr13)=",id(arr13))

arr12= [[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]
 [16 17 18 19]]
arr13= [[ 0  1]
 [ 4  5]
 [ 8  9]
 [12 13]
 [16 17]]
id(arr12)= 2327220782064
id(arr13)= 2327220781104

Stacking and Joining

Stacking is the concept of joining arrays in Numpy
Arrays having same dimensions can be stacked
The stacking is done along a new axis

Stacking can be done along three dimensions,

vstack()
- – it performs vertical stacking along the rows
- – Extends vertically

hstack()
- – it performs horizontal stacking along with the columns
- – Extends horizontally

dstack() – it performs in-depth stacking along a new third axis

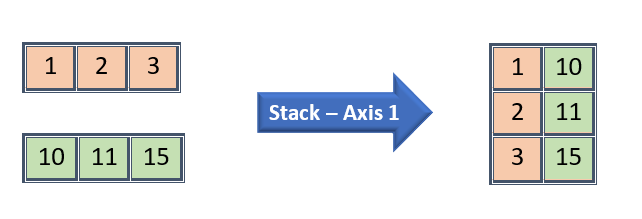
Stack – Join arrays with given axis element by element

Numpy stack function takes two input parameters – the arrays for stacking and the axis for the resultant array

Stack

Both input arrays should be in same dimension / shape
Axis parameter in stack works as dimension here instead of horizontal / vertical manner
If axis is 0, then it will join by first dimension
If axis is 1, then it will join by second dimension

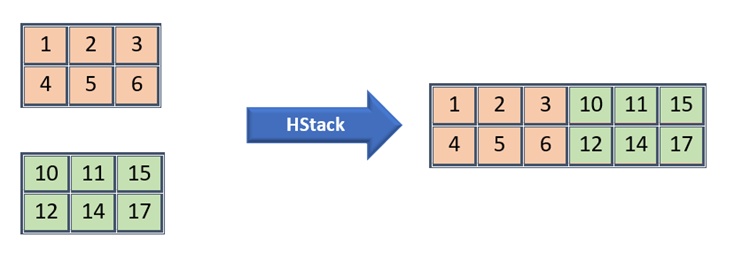
hstack – stacks horizontally

This function does not work with axis.
It extends first array by second array horizontally
As it extends horizontally, both the arrays should have same number of rows

hstack for 2D array

#hstack for 2D array
sarr5 = np.array( [ [10,20],[30,40] ])
sarr6 = np.array( [ [50,60],[70,80] ])
print(np.hstack((sarr5,sarr6)))

[[10 20 50 60]
 [30 40 70 80]]

hstack for 1 D array

#hstack for 1 D array
sarr7 = np.array([10,20,30,40])
sarr8 = np.array([90,87,10,40])
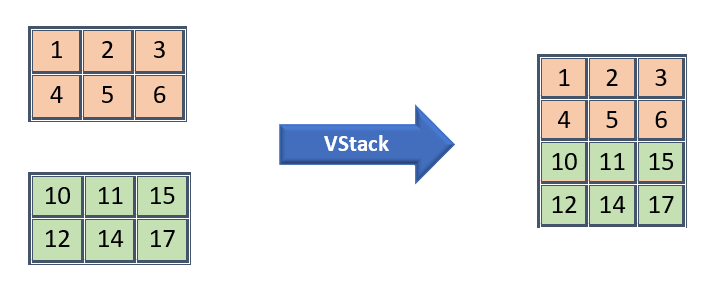
print(np.hstack((sarr8,sarr7)))

[90 87 10 40 10 20 30 40]

vstack – stacks vertically

This function does not work with axis.
It extends first array by second array vertically

vstack for 1d array

# vstack for 1d array
sarr9 = np.array([3,2,4,1,10])
sarr10 = np.array([100,200,50,300,400])
print(np.vstack((sarr9,sarr10)))

[[  3   2   4   1  10]
 [100 200  50 300 400]]

vstack for 2d array

#vstack for 2d array
sarr11 = np.array([ [2,4,6],[3,6,9]])
sarr12 = np.array( [[4,8,12],[5,15,20]])
result_vstack=np.vstack((sarr11,sarr12))
print("result_vstack=",result_vstack)

result_vstack= [[ 2  4  6]
 [ 3  6  9]
 [ 4  8 12]
 [ 5 15 20]]

When to use hstack and vstack

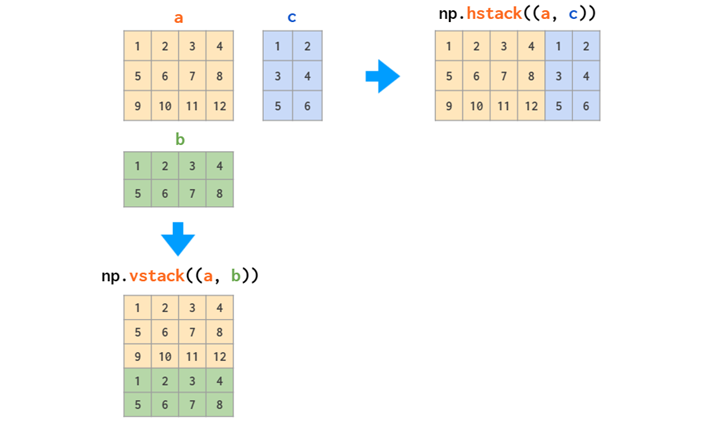
np.concatenate

numpy.vstack: stack arrays in sequence vertically (row wise).

Equivalent to np.concatenate(a,axis=0)

numpy.hstack: stack arrays in sequence horizontally (column wise).

Equivalent to np.concatenate(a,axis=1)

Syntax:

numpy.concatenate((a1, a2, ...), axis=0

a1,a2,..: sequence of array
axis : int, optional; (default is 0)

#concatenate
sarr15 = np.array([[1, 2], [3, 4]])
sarr16 = np.array([[5, 6]])
print("axis=0",np.concatenate((sarr15, sarr16), axis=0)) #increase number of rows
print("axis = 1",np.concatenate((sarr15, sarr16.T), axis=1)) #increase number of columns
print("No axis",np.concatenate((sarr15, sarr16), axis=None))

axis=0 [[1 2]
 [3 4]
 [5 6]]
axis = 1 [[1 2 5]
 [3 4 6]]
No axis [1 2 3 4 5 6]

np.append

Append is used for appending the values at the end of the array
Whereas concatenate is used for joining the sequence of array along an existing axis
Append function all the inputs must be same dimension

Syntax

numpy.append(arr, values, axis=None)

arr : values are appended to the end of the array

values: these values are appended to copy of arr

axis: int , optional

Axis along which values are appended . If axis is not given, both arr and values are flattened before use

Returns: append: a copy of arr with values appended to axis

#append
sarr13 = np.array([1,2,3])
sarr14 = np.array([[4,5,6],[7,8,9]])
print("appended array",np.append(sarr13,sarr14))

appended array [1 2 3 4 5 6 7 8 9]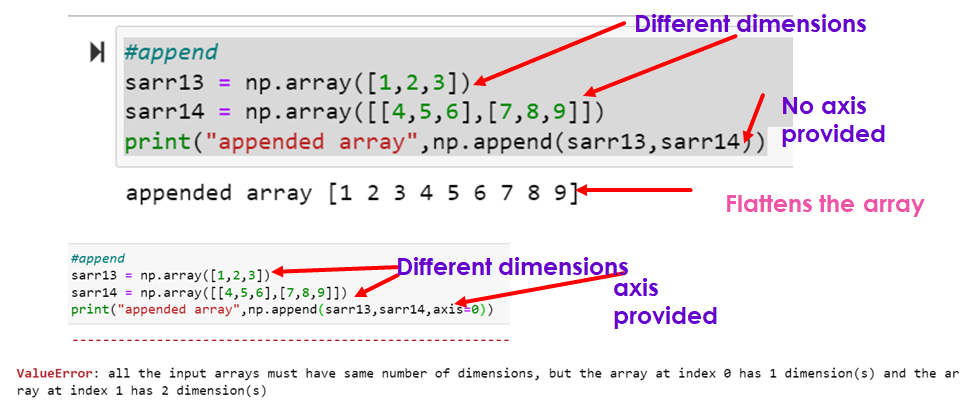

#append
sarr13 = np.array([[1,2,3],[10,20,30]])
sarr14 = np.array([[4,5,6],[7,8,9]])
print("appended array",np.append(sarr13,sarr14,axis=0)) # increase number of rows
print("appended array",np.append(sarr13,sarr14,axis=1)) # increase number of columns

appended array [[ 1  2  3]
 [10 20 30]
 [ 4  5  6]
 [ 7  8  9]]
appended array [[ 1  2  3  4  5  6]
 [10 20 30  7  8  9]]

Matrix in numpy

Matrix is a subclass within ndarray class in the Numpy python library.

Syntax:

numpy.matrix(data, dtype, copy)

Data: Data should be in the form of an array-like an object or a string separated by commas

Dtype: Data type of the returned matrix

Matrix Operations

np.argmax

numpy.clip

numpy.clip(a, a_min, a_max, out=None)

Clip (limit) the values in an array
Given an interval, values outside the interval are clipped to the interval edges

For example, if an interval of [0,1] is specified, values smaller than 0 become 0 and values larger than 1 become 1

a: array conaining elements to clip
a_min, a_max: Minimum and maximum value
out: result will be placed in this array

ma9 = np.matrix('10,20,30,40,50,5')
print("The clipped array:\n",np.clip(ma9,4,20))

The clipped array:
 [[10 20 20 20 20  5]]

np.diagonal

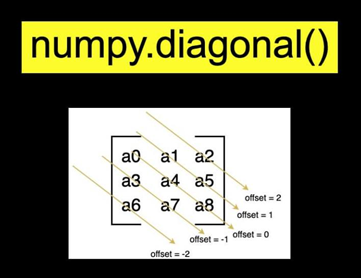
numpy.diagonal(a, offset=0)
A: 2D array
offset: represents position

sa1 = 4*np.arange(12).reshape(4,3)
print("Array:\n",sa1)
print("Main diagonal: \n",np.diagonal(sa1))
print("Diagonal at offset = 1: \n",np.diagonal(sa1,offset = 1))
print("Diagonal at offset = -1: \n",np.diagonal(sa1,offset = -1))

Array:
 [[ 0  4  8]
 [12 16 20]
 [24 28 32]
 [36 40 44]]
Main diagonal: 
 [ 0 16 32]
Diagonal at offset = 1: 
 [ 4 20]
Diagonal at offset = -1: 
 [12 28 44]

Matrix Operations

Matrix multiplications

multiply( ): element – wise matrix multiplication
matmul( ): matrix product of two arrays
dot(): dot product o two arrays

Matrix Multiplication

np.matmul()

Matrix product of two given arrays

Syntax:

np.matmul(array a, array b)

Input to this function cannot be scalar

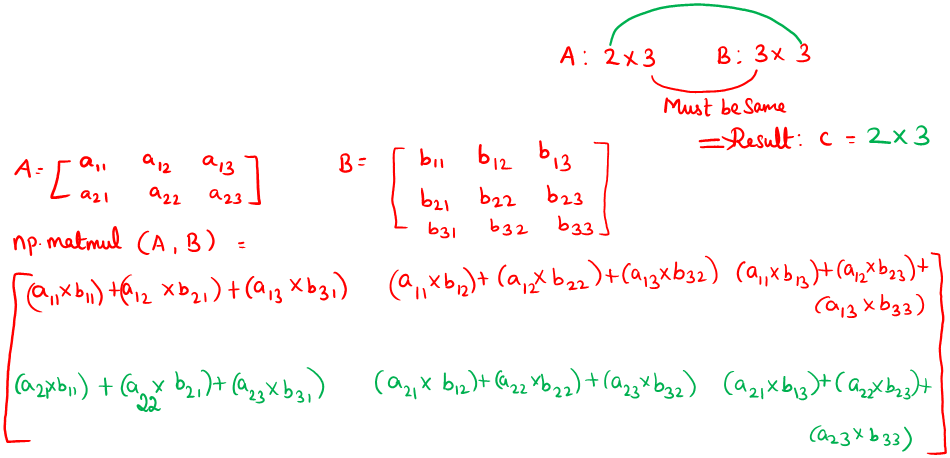
#matmul() - Matrix multiplication
ma = np.array([[1,2,3],[4,5,6]])
mb = np.array([[10,20,30],[40,50,60],[70,80,90]])
print("Matrix A: \n",ma)
print("Matrix B: \n",mb)
mc = np.matmul(ma,mb)
print("Result :\n",mc)

Matrix A: 
 [[1 2 3]
 [4 5 6]]
Matrix B: 
 [[10 20 30]
 [40 50 60]
 [70 80 90]]
Result :
 [[300 360 420]
 [660 810 960]]

np.multiply()

Element wise product of two given arrays

Syntax:

np.multiply(array a, array b)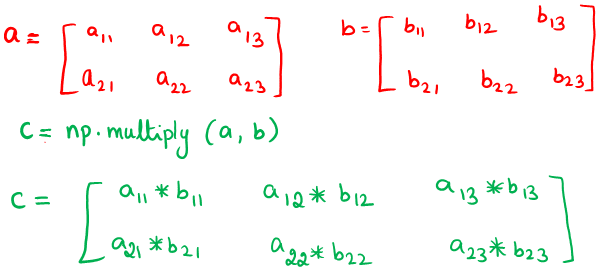

#multiply() - Element wise multiplication
ma1 = np.array([[1,2,3],[4,5,6]])    # number of columns must be equal 
mb1 = np.array([[10,20,30],[40,50,60]])
print("Matrix A: \n",ma1)
print("Matrix B: \n",mb1)
mc1 = np.multiply(ma1,mb1)
print("Result :\n",mc1)

Matrix A: 
 [[1 2 3]
 [4 5 6]]
Matrix B: 
 [[10 20 30]
 [40 50 60]]
Result :
 [[ 10  40  90]
 [160 250 360]]

np.dot()

The dot product of any two given matrices is basically their matrix product
The only difference in dot product, we can have scalar values

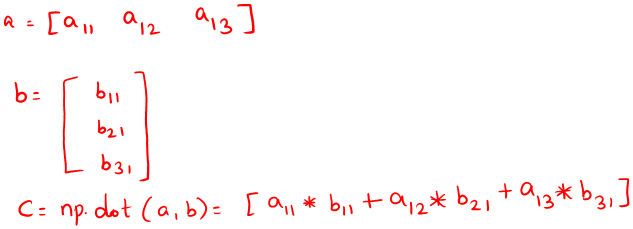
#dot() - Matrix multiplication
ma2 = np.array([[1,2,3],[4,5,6]])
mb2 = np.array([[10,20,30],[40,50,60],[70,80,90]])
print("Matrix A: \n",ma2)
print("Matrix B: \n",mb2)
mc2 = np.dot(ma2,mb2)
print("Result :\n",mc2)

Matrix A: 
 [[1 2 3]
 [4 5 6]]
Matrix B: 
 [[10 20 30]
 [40 50 60]
 [70 80 90]]
Result :
 [[300 360 420]
 [660 810 960]]

#dot() - Matrix multiplication
ma3 = np.array([1,2,3])
mb3 = np.array([10,20,30])
print("Matrix A: \n",ma3)
print("Matrix B: \n",mb3)
mc3 = np.dot(ma3,mb3)
print("Result :\n",mc3)

Matrix A: 
 [1 2 3]
Matrix B: 
 [10 20 30]
Result :
 140

#dot() - Matrix multiplication
ma4 = np.array([[1,2,3],[4,5,6]])
print("Matrix A: \n",ma4)
mc4 = np.dot(2,ma4)
print("Result :\n",mc4)

Matrix A: 
 [[1 2 3]
 [4 5 6]]
Result :
 [[ 2  4  6]
 [ 8 10 12]]

Linear Algebra operations

dot( ) – calculate dot product of two arrays

vdot() – calculate do product of two vectors

inner() – calculate inner product of arrays

outer() – computes the outer product of two arrays

det() – calculate determinant of matrix

solve() – solve linear matrix equation

inv() – calculate multiplicative inverse of the matrix

trace() – sum of diagonal elements

urank() – returns the rank of the matrix

np.vdot()

Returns the dot product of vectors a and b

#vdot
va = np.array([[1,2,3],[10,20,30]])
vb = np.array([[2,4,6],[4,3,2]])
print("Matrix:\n",va)
print("Matrix:\n",vb)
result_dot = np.vdot(va,vb)
print("Result=",result_dot)

Matrix:
 [[ 1  2  3]
 [10 20 30]]
Matrix:
 [[2 4 6]
 [4 3 2]]
Result= 188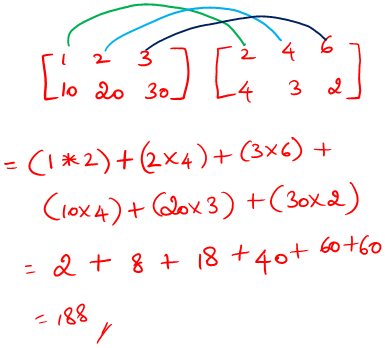

np.inner()

Computes the inner product of two arrays

np.inner(a, b) = sum(a[:] * b[:])

#inner
va1 = np.array([[10,20],[1,4]])
va2 = np.array([[1,2],[2,5]])
print("Matrix:\n",va1)
print("Matrix:\n",va2)
result_inner= np.inner(va1,va2)
print("result =",result_inner)

Matrix:
 [[10 20]
 [ 1  4]]
Matrix:
 [[1 2]
 [2 5]]
result = [[ 50 120]
 [  9  22]]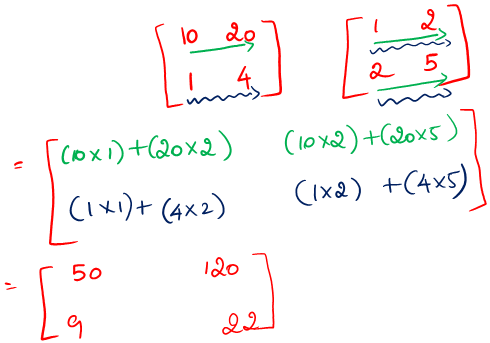

np.outer()

numpy.outer(a, b)
a,b: input array

#outer
va1 = np.array([[10,20],[1,4]])
va2 = np.array([[1,2],[2,5]])
print("Matrix:\n",va1)
print("Matrix:\n",va2)
result_outer= np.outer(va1,va2)
print("result =",result_outer)

Matrix:
 [[10 20]
 [ 1  4]]
Matrix:
 [[1 2]
 [2 5]]
result = [[ 10  20  20  50]
 [ 20  40  40 100]
 [  1   2   2   5]
 [  4   8   8  20]]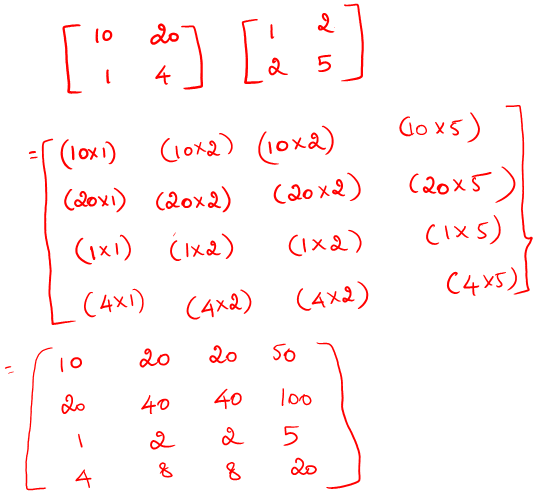

np.linalg.det()

np.linalg.det(a)
a:matrix

#detfrom numpy import linalg
va3 = np.array([[1,2],[4,5]])
print("Determinant of matrix=",np.linalg.det(va3))

Determinant of matrix= -2.9999999999999996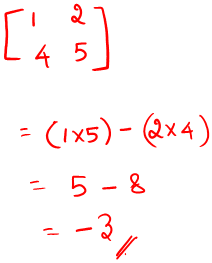

np.linalg.solve

linalg.solve(a, b)

a: coefficient values
b: dependent matrix

#solve the linear equation 3x+2y = 3; 2x+3y = 7
va4 = np.array([[3,2],[2,3]])
va5 = np.array([3,7])
print(np.linalg.solve(va4,va5))

[-1.  3.]

np.linalg.matrix_power

Raises a square matrix integer to the power n

linalg.matrix_power(a, n)

a: array
n: integer

#matrix_power
va7 = np.array([[1,2],[4,6]])
print(np.linalg.matrix_power(va7,2))

[[ 9 14]
 [28 44]]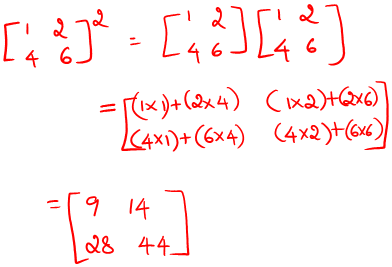

np.linalg.solve

#Trace of a
va6 = np.array([[2,4,3],[1,3,-1],[8,-9,-10]])
print("Trace=",np.trace(va6))

-5

np.trace

Mathematical Operations

Trignometric functions

np.sin() – performs trigonometric sine calculation element wise

np.cos() – performs trigonometric cosine calculation element wise

np.tan() – performs trigonometric tangent calculation element wise

np.arcsin() – performs trigonometric inverse sine element-wise

np.arccos() – performs trigonometric inverse of cosine element-wise

np.arctan() – performs trigonometric inverse of tangent element-wise

Hyperbolic functions

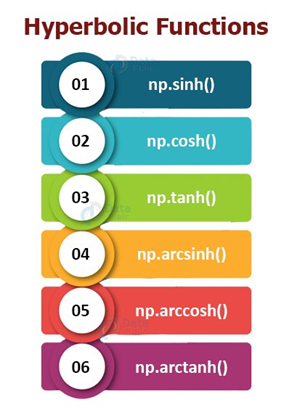
01. Returns the hyperbolic sine of the array elements

02. Returns the hyperbolic cosine of the array elements

03. Returns the hyperbolic sine of the array elements

04. Returns the hyperbolic inverse sine of the array elements

05. Returns the hyperbolic inverse cosine of the array elements

06. Returns the hyperbolic inverse tan of the array elements

Rounding Functions

np.around

#Rounding Functions
ra = np.array([20.39999,45.4321,1.32456])
print(np.around(ra,2))

[20.4  45.43  1.32]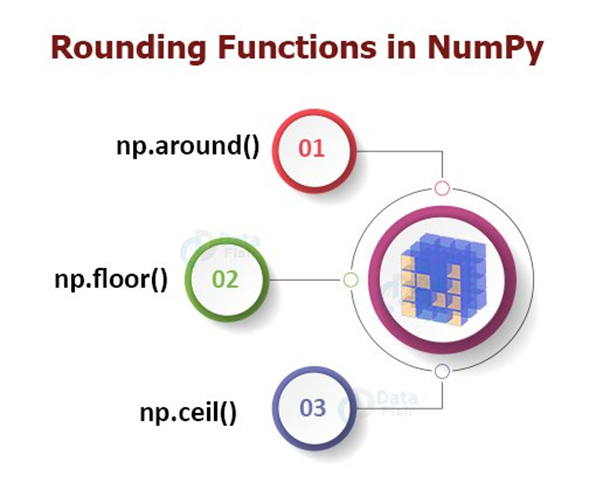

Used to round off a decimal number to desired number of positions

Takes two parameters: the input number and precision of decimal places

#floor
print(np.floor(ra))

[20.   45.   1.]

Returns the floor value of the input decimal value
Returns the largest integer number less than the input value

#ceil
print(np.ceil(ra))

[21.   46.   2.]

Returns the ceil value of the input decimal value
Returns the smallest integer number greater than the input value

Numpy Exponential and logarithmic functions

np.exp()

Calculates exponential of the input array elements

np.log()

Calculates the natural log of the input array elements Natural logarithm of a value is the inverse of its exponential value

Numpy complex functions

np.isreal()

Returns the output of a test for real numbers

#COMPLEX FUNCTIONS
arrc = np.array([1,2,3])
print(np.isreal(arr))
arrc1 = np.array([1+2j])
print(np.isreal(arrc1))

[ True  True  True]
[False]

np.conj()

Useful for calculation of conjugate of complex numbers

arrc2 =np.array([1+2j,2,3])
print(np.conj(arrc2))

[1.-2.j 2.-0.j 3.-0.j]

Searching, Sorting and Counting

Searching

To find the place of a element or value in the array
Depending on the element being found or not found, a search is said to be successful or unsuccessful

Searching

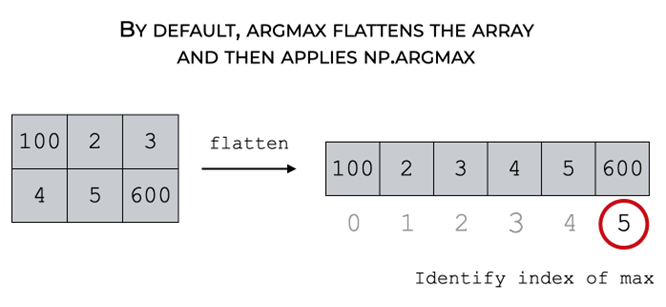
np.argmax( )

Returns the indices of the max element of array in a particular axis

Syntax:

np.argmax(array, axis)

ea = np.array([[5,2,10],[4,3,1],[19,0,8]])
print("the index for maximum element in array is:",np.argmax(ea))
print("matrix:\n",ea)
print("the index for maximum element in array along axis = 0 is:",np.argmax(ea,axis=0))#along column
print("the index for maximum element in array along axis = 1 is:",np.argmax(ea,axis=1))#along row

the index for maximum element in array is: 6
matrix:
 [[ 5  2 10]
 [ 4  3  1]
 [19  0  8]]
the index for maximum element in array along axis = 0 is: [2 1 0]
the index for maximum element in array along axis = 1 is: [2 0 0]

np.nanargmax

Function that will return indices of the max element of array in a specified axis while ignoring NaNs

Syntax:

np.nanargmax(array, axis)

ea1 = np.array([[np.nan,40,10],[10,np.nan,1]])
print("matrix:\n",ea1)
print("the index for maximum element in array is:",np.nanargmax(ea1))
print("the index for maximum element in array along axis = 0 is:",np.nanargmax(ea1,axis=0))#along column
print("the index for maximum element in array along axis = 1 is:",np.nanargmax(ea1,axis=1))#along row

matrix:
 [[nan 40. 10.]
 [10. nan  1.]]
the index for maximum element in array is: 1
the index for maximum element in array along axis = 0 is: [1 0 0]
the index for maximum element in array along axis = 1 is: [1 0]

np.argmin

Returns the index of the minimum value in array list

Syntax:

np.argmin(array,axis)

ea2 = np.array([[5,2,10],[4,3,1],[19,0,8]])
print("the index for minimum element in array is:",np.argmin(ea2))
print("matrix:\n",ea2)
print("the index for minimum element in array along axis = 0 is:",np.argmin(ea2,axis=0))#along column
print("the index for minimum element in array along axis = 1 is:",np.argmin(ea2,axis=1))#along row

the index for minimum element in array is: 7
matrix:
 [[ 5  2 10]
 [ 4  3  1]
 [19  0  8]]
the index for minimum element in array along axis = 0 is: [1 2 1]
the index for minimum element in array along axis = 1 is: [1 2 1]

np.nanargmin

Function that will return indices of the min element of array in a specified axis while ignoring NaNs

Syntax:

np.nanargmin(array, axis)

ea3 = np.array([[np.nan,40,10],[10,np.nan,1]])
print("matrix:\n",ea3)
print("the index for minimum element in array is:",np.nanargmin(ea1))
print("the index for minimum element in array along axis = 0 is:",np.nanargmin(ea1,axis=0))#along column
print("the index for minimum element in array along axis = 1 is:",np.nanargmin(ea1,axis=1))#along row

matrix:
 [[nan 40. 10.]
 [10. nan  1.]]
the index for minimum element in array is: 5
the index for minimum element in array along axis = 0 is: [1 0 1]
the index for minimum element in array along axis = 1 is: [2 2]

np.extract()

Returns elements of input array if they satisfied some condition

Syntax:

numpy.extract(condition,array)

Condition: condition on the basis of which user extracts elements

Returns: array elements that satisfy the condition

#np.extract:
ea4 = np.arange(4,64,4).reshape(5,3)
print("Array:",ea4)
#selecting the array elements that are divided by 5
condition1 = np.mod(ea4,5) == 0
print("condition=",condition1)
ea5 = np.extract(condition1,ea4)
print("Extracted array:",ea5)
#selecting the array elements that are less than user specified value
condition2 = np.logical_and(ea4 > 3, ea4 < 10)
print("condition=",condition2)
ea6 = np.extract(condition2,ea4)
print("Extracted array:",ea6)

Array: [[ 4  8 12]
 [16 20 24]
 [28 32 36]
 [40 44 48]
 [52 56 60]]
condition= [[False False False]
 [False  True False]
 [False False False]
 [ True False False]
 [False False  True]]
Extracted array: [20 40 60]
condition= [[ True  True False]
 [False False False]
 [False False False]
 [False False False]
 [False False False]]
Extracted array: [4 8]

np.nonzero()

Syntax:

np.nonzero(A)

Returns the indices of the non zero elements in the array

#np.nonzero()
x = np.array([[3, 0, 0], [0, 4, 0], [5, 6, 0]])
print("in 2 d array the elements at",np.nonzero(x)) # returns the row number of non zero element as an array and column number as separate array
# to view the elements
print("non zero elements are:\n",x[np.nonzero(x)])
# to view the index
print("In 2 array the non zero elements are at the index:",np.transpose(np.nonzero(x)))
x1 = np.array([2,3,4,0,10,0])
print("in 1 d array:",np.nonzero(x1)) # returns the index of non zero element

in 2 d array the elements at (array([0, 1, 2, 2], dtype=int64), array([0, 1, 0, 1], dtype=int64))
non zero elements are:
 [3 4 5 6]
In 2 array the non zero elements are at the index: [[0 0]
 [1 1]
 [2 0]
 [2 1]]
in 1 d array: (array([0, 1, 2, 4], dtype=int64),)

np.where()

Syntax:

np.where(condition, [x,y])

Two parameters x and y; If conditions holds true for some element in the array, the new array will choose elements from x.

Otherwise if it is false, elements from y will be taken

X and y are optional. But if you specify x, you must also specify y.

#np.where()
#extract only positive elements
r = int(input("enter the number of rows"))
c = int(input("enter the number of columns"))
arc = []
for i in range(r):
    rrr = []
    for j in range(c):
        rrr.append(int(input()))
    arc.append(rrr)
arra = np.array(arc) # creating array from user input
print("Here is the array:\n",arra)
#Get only positive values
ar_pos = np.where(arra>0, arra,0)
print(ar_pos)

enter the number of rows3
enter the number of columns3
-2
-2
-1
3
4
0
1
1
-1
Here is the array:
 [[-2 -2 -1]
 [ 3  4  0]
 [ 1  1 -1]]
[[0 0 0]
 [3 4 0]
 [1 1 0]]

np.argwhere

Return the indices on satisfying condition

Syntax:

np.argwhere(condition)

#find the index where the codition is true
arg1 = ([2,4,6],[8,10,12],[14,16,18])
print(np.argwhere(np.mod(arg1,4)==0))

[[0 1]
 [1 0]
 [1 2]
 [2 1]]

np.flatnonzero()

Used to compute indices that are non-zero in the flattened version of arr

Syntax:

np.flatnonzero(arr)

arr: input array

Output: ndarray ; containing the indices of the elements

#np.flatnonzero()
arg1 = ([-2,-4,0],[0,10,12],[14,16,18])
print(np.flatnonzero(arg1))

[0 1 4 5 6 7 8]

Sorting

np.sort()

Returns an array in sorted format

numpy.sort(a, axis=- 1, kind=None)

a: array to be sorted

axis: int or none, optional

axis along which to sort. If none the array is flattened before sorting. The default is -1, which sorts along the last axis

kind: {‘quicksort’, ‘mergesort’, ’heapsort’, ‘stable’}

arg1 = ([-2,-4,0],[-36,100,12],[140,16,18])
print(np.sort(arg1)) # sorts the element in each row separately
print("When axis = 0: \n",np.sort(arg1,axis = 0))
print("When axis = 1: \n",np.sort(arg1,axis = 1))# sorts the element in each row separately
print("When axis = none: \n",np.sort(arg1,axis = None))
print("When axis = -1 : \n",np.sort(arg1,axis = -1))

[[ -4  -2   0]
 [-36  12 100]
 [ 16  18 140]]
When axis = 0: 
 [[-36  -4   0]
 [ -2  16  12]
 [140 100  18]]
When axis = 1: 
 [[ -4  -2   0]
 [-36  12 100]
 [ 16  18 140]]
When axis = none: 
 [-36  -4  -2   0  12  16  18 100 140]
When axis = -1 : 
 [[ -4  -2   0]
 [-36  12 100]
 [ 16  18 140]]

Counting functions

np.char.count()

Returns an array with the number of non-overlapping occurences (unique) of a given substring in the range [start,end]

Syntax:

np.char.count(a,sub,start,ed=None)

a: input array or an input string

sub: parameter indicating the substring to search from the input string to the input array

Start,end: optional parameters, both start and end are used to set the boundary within which the substring is to be searched Returns: an integer array with the number of non overlapping occurences of the substring

cou = np.array(['qwertyqwertyqwyerta','afehhghogrta','ababababacta'])
print(cou)
print("The occurence of q is", np.char.count(cou,"q"))
print("the occurence of ta is",np.char.count(cou,'ta'))
print("the occurence of ta is",np.char.count(cou,'ta',17,19))# stop is exclusive

np.char.count()

Count number of times a particular value present in the array:

#counting the values
cou1 = np.array([20,13,2,4,5,1,4,3,4])
sear = int(input("Enter the input:"))
count = (cou1==sear).sum()
print("Number of times:",count)

Enter the input:4
Number of times: 3

String Functions

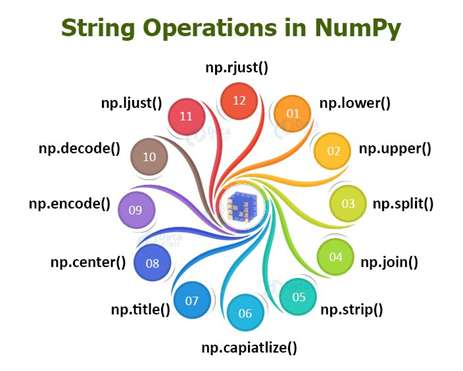
np.char.lower() – converts all the uppercase characters in the string to lower case

np.char.upper() – converts all the lowercase characters in the string to lower case

np.char.split() –Breaks the string

np.char.join() – joins the array by a particular separator

np.char.strip() – strip off all leading and trailing whitespaces from a string

np.char.capitalize() – Capitalize the first character of the string

np.char.title( ) – capitalize the first character

str1= np.array(['apple','guava','banana',"    Mango yummy"])
print("lowercase:\n",np.char.lower(str1))
print("uppercase:\n",np.char.upper(str1))
print("SPlit:\n",np.char.split(str1))
print("join:\n",np.char.join("-",str1))
print("strip:\n",np.char.strip(str1))
print("capitalize:\n",np.char.capitalize(str1))
print("Title case:\n",np.char.title(str1))

lowercase:
 ['apple' 'guava' 'banana' '    mango yummy']
uppercase:
 ['APPLE' 'GUAVA' 'BANANA' '    MANGO YUMMY']
SPlit:
 [list(['apple']) list(['guava']) list(['banana']) list(['Mango', 'yummy'])]
join:
 ['a-p-p-l-e' 'g-u-a-v-a' 'b-a-n-a-n-a' ' - - - -M-a-n-g-o- -y-u-m-m-y']
strip:
 ['apple' 'guava' 'banana' 'Mango yummy']
capitalize:
 ['Apple' 'Guava' 'Banana' '    mango yummy']
Title case:
 ['Apple' 'Guava' 'Banana' '    Mango Yummy']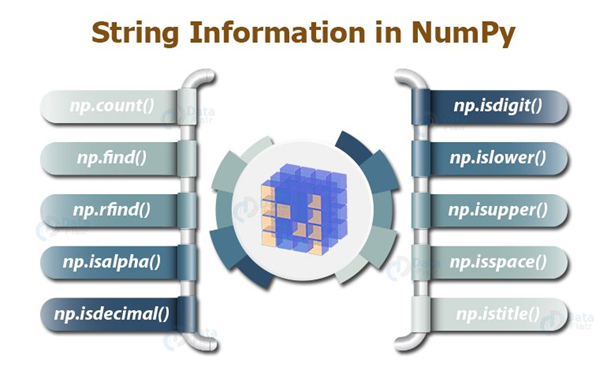

np.char.count() – returns the count of the passed substring from the entire string

np.char.find() – returns the lowest index of the substring if present in the input string

np.char.rfind() – returns the highest index of the substring if present in the input string

np.char.isnumeric() – used to detect numeric values. Returns True if all the string characters are numeric

np.char.isalpha() – used to detect alphabets. Returns true if all the string characters are alphabets

np.char.isdecimal() – used to detect decimal values. Returns true if all the string characters are decimal numbers

np.char.isdigit() – used to detect digits. Returns true if all the string characters are digits

np.char.islower() – used to find the lower case values. Reurns true if all the string characters are lowercase

np.char.isupper() – used to find the upper case values. Reurns true if all the string characters are uppercase

np.char.isspace() – returns true if all the characters of the string are white spaces otherwise returns false

np.char.istitle() – returns true only if the string is title cased

str1= np.array(['apple','guava','banana',"    Mango yummy"])
print("count of an : \n",np.char.count(str1,"an"))
print("To find lower index of occurence of a:\n",np.char.find(str1,"a"))
print("to find higher index of occurence of a: \n",np.char.rfind(str1,"a"))
print("is numberic:\n",np.char.isnumeric(str1))
print("is alphabets:\n",np.char.isalpha(str1))
str2 = np.array([1.2,2,3,'abc'])
print("is decimal:\n",np.char.isdecimal(str2))
print("is digit:\n",np.char.isdigit(str2))
print("is lower:\n",np.char.islower(str1))
print("is upper:\n",np.char.isupper(str1))
print("is space:\n",np.char.isspace(str1))
print("is title:\n",np.char.istitle(str1))

count of an : 
 [0 0 2 1]
To find lower index of occurence of a:
 [0 2 1 5]
to find higher index of occurence of a: 
 [0 4 5 5]
is numberic:
 [False False False False]
is alphabets:
 [ True  True  True False]
is decimal:
 [False  True  True False]
is digit:
 [False  True  True False]
is lower:
 [ True  True  True False]
is upper:
 [False False False False]
is space:
 [False False False False]
is title:
 [False False False False]

np.char.equal() – checks element wise equivalence. Returns true, only if all elements are equal

np.char.not_equal() – checks whether two string are equal or not

np.char.greater() – returns true if the first string is greater than the second string

np.char.less() – returns true if the first string is less than the second string

np.char.greater_equal() – Returns true if the first string is greater than or equal to the second string

np.char.less_equal() – Returns true if the first string is less than or equal to the second string

str1= np.array(['apple','guava','banana',"Mango yummy"])
str3 = np.array(['apple','Guave','banana',"Mango Yummy"])
print("Equal:\n", np.char.equal(str1,str3))
print("Check for inequality:\n",np.char.not_equal(str1,str3))
print("Greater:\n",np.char.greater(str1,str3))
print("Lesser:\n",np.char.less(str1,str3))
print("Greater or equality:\n",np.char.greater_equal(str1,str3))
print("Lesser or equality:\n",np.char.less_equal(str3,str1))

Equal:
 [ True False  True False]
Check for inequality:
 [False  True False  True]
Greater:
 [False  True False  True]
Lesser:
 [False False False False]
Greater or equality:
 [ True  True  True  True]
Lesser or equality:
 [ True  True  True  True]

Advanced Python

Numpy Operations

Arithmetic functions

Broadcasting Rules

Addition

Subtraction

Multiplication

Division

Reciprocal

Power

Modulus

Statistical Functions

np.amin

Syntax

Returns

Finding Minimum

np.amax

Syntax

Finding Maximum

np.mean

Syntax

np.median

numpy.ptp

Syntax

Returns

np.var

Formula

Syntax

np.std

Syntax

np.percentile

Bitwise Operators

Bitwise And Operator

np.bitwise_and

np.bitwise_or

np.bitwise_and and np.bitwise_or

np.bitwise_invert()

np.invert()

np.bitwise_xor

np.left_shift

np.right_shift()

Copying and Viewing Array

No Copy at All

View or shallow copy

Deep Copy

Stacking and Joining

Stack

hstack – stacks horizontally

hstack for 2D array

hstack for 1 D array

vstack – stacks vertically

vstack for 1d array

vstack for 2d array

When to use hstack and vstack

np.concatenate

Syntax:

np.append

Syntax

Matrix in numpy

Syntax:

Matrix Operations

np.argmax

numpy.clip

np.diagonal

Matrix Operations

Matrix multiplications

Matrix Multiplication

np.matmul()

Syntax:

np.multiply()

Syntax:

np.dot()

Linear Algebra operations

np.vdot()

np.inner()

np.outer()

np.linalg.det()

np.linalg.solve

np.linalg.matrix_power

np.linalg.solve