K-Mean and K-Nearest Neighbor

Clustering

Cluster: A collection of data objects

• similar (or related) to one another within the same group
• dissimilar (or unrelated) to the objects in other groups

Cluster analysis (or clustering, data segmentation, …)

• Finding similarities between data according to the characteristics found in the data and grouping similar data objects into clusters

Unsupervised learning: no predefined classes (i.e., learning by observations vs. learning by examples: supervised)

Typical applications

• As a stand-alone tool to get insight into data distribution
• As a preprocessing step for other algorithms

K-Means

• Nonhierarchical, each instance is placed in exactly one of K nonoverlapping clusters.
• Since only one set of clusters is output, the user normally has to input the desired number of clusters K.

1. Decide on a value for k. 
2. Initialize the k cluster centers (randomly, if necessary). 
3. Decide the class memberships of the N objects by assigning them to the nearest cluster center. 
4. Re-estimate the k cluster centers, by assuming the memberships found above are correct. 
5. If none of the N objects changed membership in the last iteration, exit. Otherwise goto 3.

Evaluation of K-Means

Strength

• Relatively efficient: O(tkn), where n is # objects, k is # clusters, and t  is # iterations. Normally, k, t << n.
• Often terminates at a local optimum. The global optimum may be found using techniques such as: deterministic annealing and genetic algorithms

Weakness

• Applicable only when mean is defined, then what about categorical data?
• Need to specify k, the number of clusters, in advance
• Unable to handle noisy data and outliers
• Not suitable for clusters with non-convex shapes

Before and After K-Means

K-Means Algorithm

Algorithm:

k-means, algorithm for partitioning, where each cluster’s center is represented by the mean value of the objects in the cluster.

Input:

• k: the number of clusters
• D: a data set containing n objects

Output:

A set of k clusters

Method:

1. Arbitrarily choose k objects from D as the initial cluster centers;
2. repeat
3. (re)assign each object to the cluster to which the object is the most similar, based on the mean value of the objects in the cluster;
4. update the cluster means, i.e., calculate the mean value of the objects for each cluster;
5. until no change;

Example: K-Means

K-Nearest Neighbor

• K-Nearest Neighbour is one of the simplest Machine Learning algorithms based on Supervised Learning technique.
• K-NN algorithm assumes the similarity between the new case/data and available cases and put the new case into the category that is most similar to the available categories.
• K-NN algorithm stores all the available data and classifies a new data point based on the similarity. This means when new data appears then it can be easily classified into a well suite category by using
• K- NN algorithm. K-NN algorithm can be used for Regression as well as for Classification but mostly it is used for the Classification problems.
• K-NN is a non-parametric algorithm, which means it does not make any assumption on underlying data.
• It is also called a lazy learner algorithm because it does not learn from the training set immediately instead it stores the dataset and at the time of classification, it performs an action on the dataset.
• KNN algorithm at the training phase just stores the dataset and when it gets new data, then it classifies that data into a category that is much similar to the new data.

Why K-NN

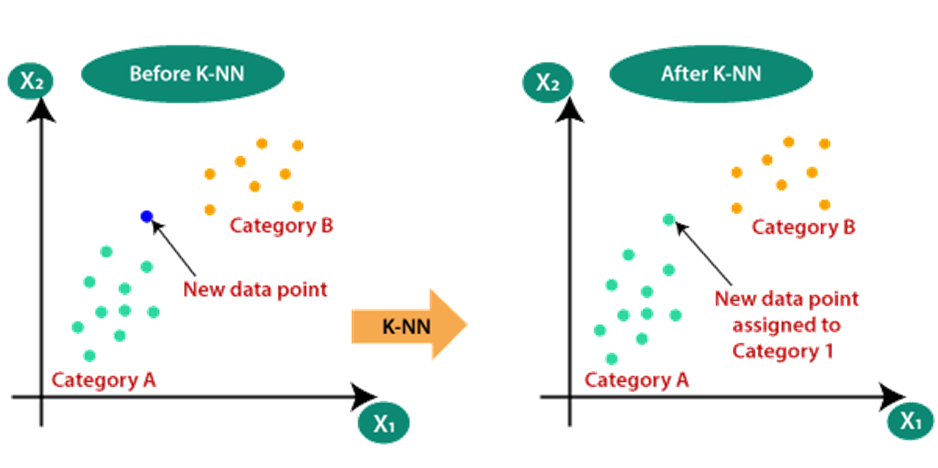
Working of K-NN

The K-NN working can be explained on the basis of the below algorithm:

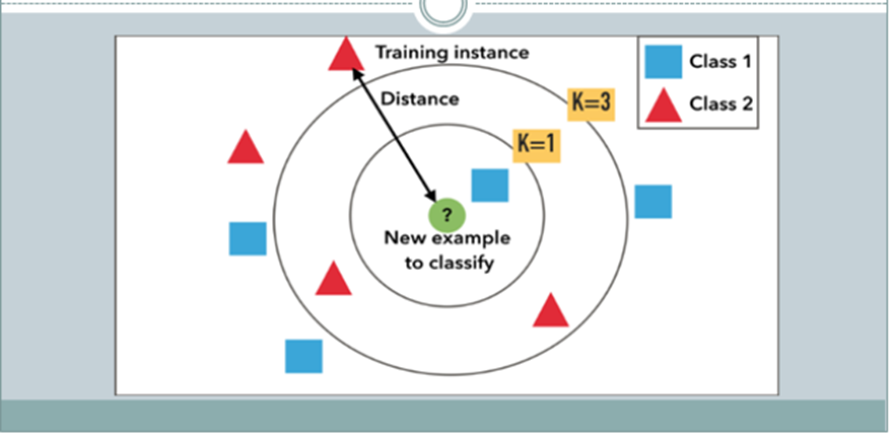
Step-1: Select the number K of the neighbors

Step-2: Calculate the Euclidean distance of K number of neighbors

Step-3: Take the K nearest neighbors as per the calculated Euclidean distance.

Step-4: Among these k neighbors, count the number of the data points in each category.

Step-5: Assign the new data points to that category for which the number of the neighbor is maximum.

Euclidean Distance

How to Choose K?

.

There is no particular way to determine the best value for “K”, so we need to try some values to find the best out of them. The most preferred value for K is 5.

A very low value for K such as K=1 or K=2, can be noisy and lead to the effects of outliers in the model.

Advantages of K-NN

• It is simple to implement.
• It is robust to the noisy training data
• It can be more effective if the training data is large.

Drawbacks of K-NN

• Always needs to determine the value of K which may be complex some time.
• The computation cost is high because of calculating the distance between the data points for all the training samples.

Various Distance Functions

Distance Functions

K-NN Algorithm

Training Algorithm:

For each training example (x, f(x)), add the example to the list training_examples

Classification Algorithm:

Given the query instance x_q to be classified,

Let x₁….x_k denote the k instances from training_example that are nearest to x_q

Return

Where,

Where,

Example – K-NN

Solution

Views: 4