Regression
- A regression model is a mathematical equation that describes the relationship between two or more variables
- A simple regression model includes only two variables: one independent and one dependent.
- The dependent variable is the one being explained and the independent variable is the one used to explain the variation in the dependent variable
Remember this:
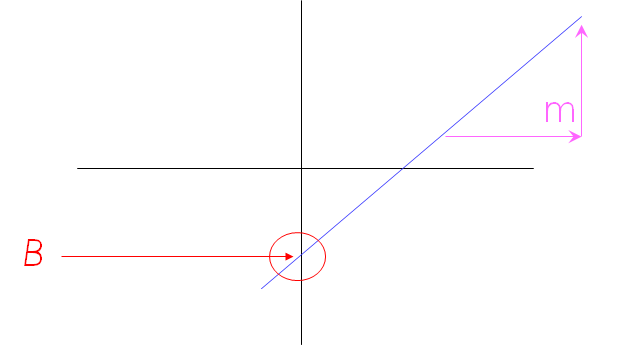
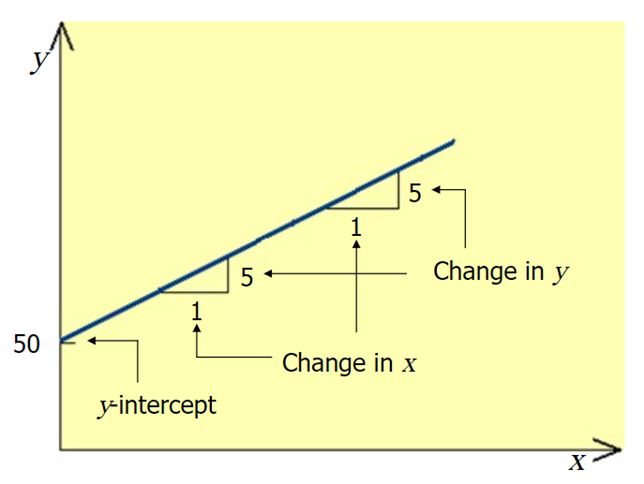
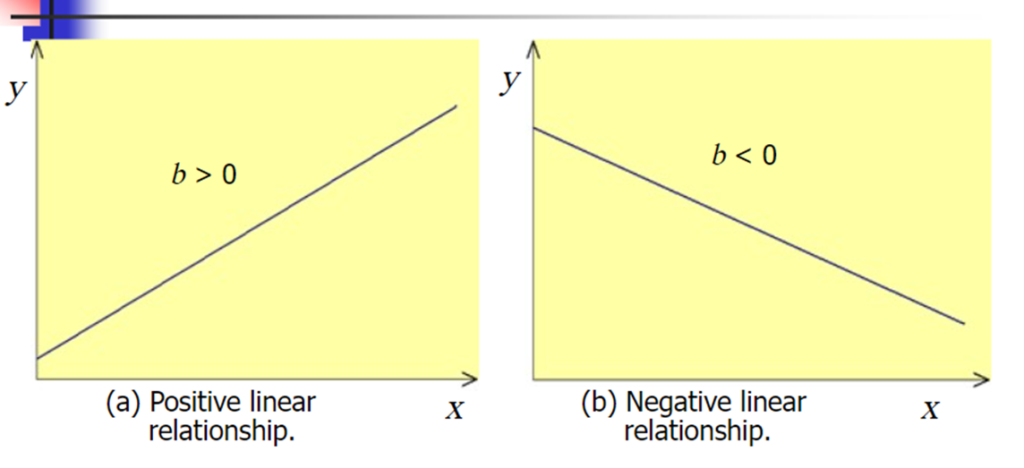
A slope of 2 means that every 1-unit change in X yields a 2-unit change in Y.
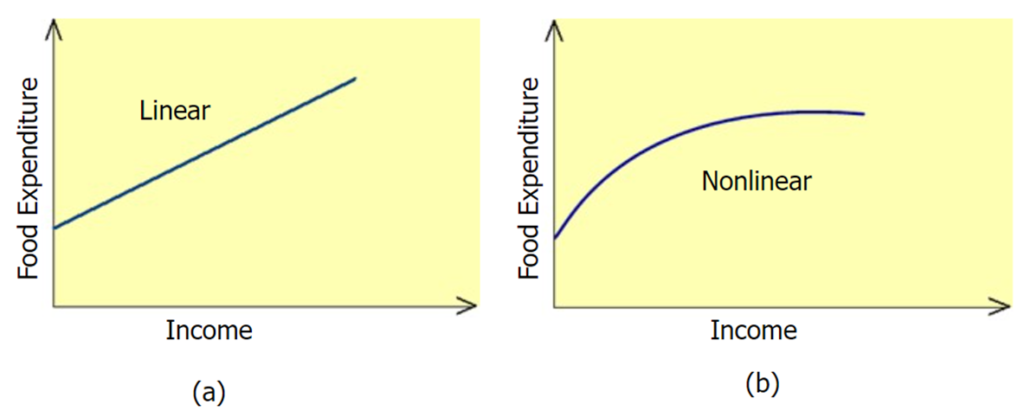
Linear Regression
A (simple) regression mode that gives a straight-line relationship between two variables is called a linear regression model
Simple Linear Regression Analysis
- Scatter Diagram
- Least Square Line
- Interpretation of slope and intercept
- Assumptions of Regression Analysis
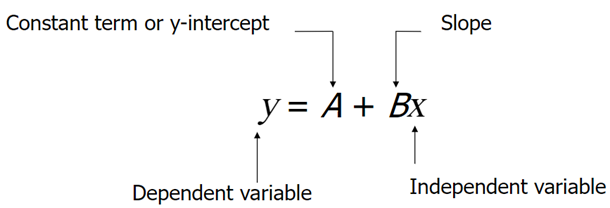

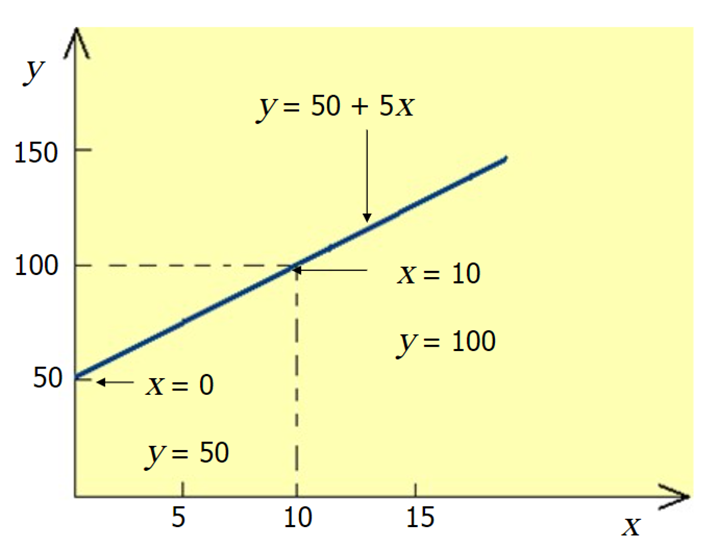
In the regression model, y= A+Bx+C
- A is called the y-intercept or constant term
- B is the slope
- C is the random error
- The dependent and independent variables are y and x respectively
Sum of Squared Error (SSE)
The sum of Squared error (SSE) is,
The values of a and b that gives the minimum SSE are called least square estimates and the regression line obtained with these estimates is called the least square line
The Least Squares line
For the least squares regression line,
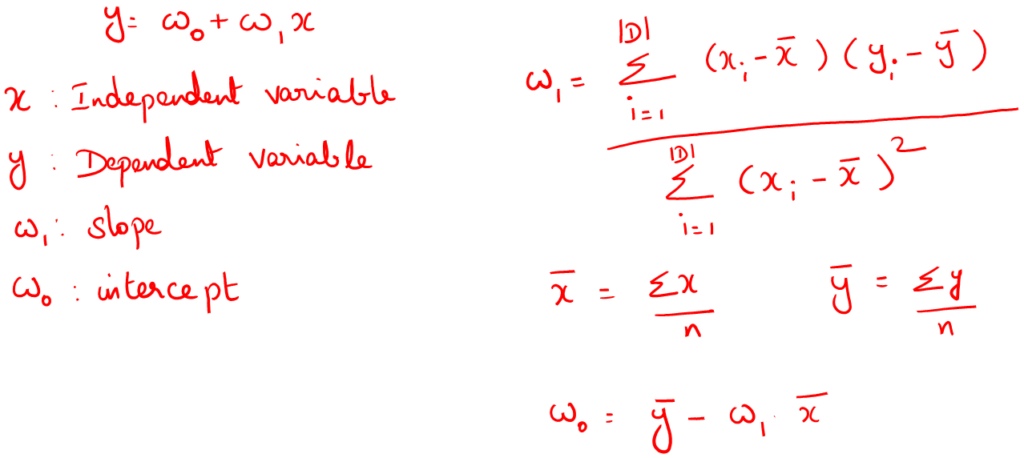
Interpretation of slope and intercept
The value of intercept in the regression model gives the change in y due to change of one unit in x
Assumptions of the Regression Model
- Assumption 1: The random error has a mean equal to zero for each x
- Assumption 2: The errors associated with different observations are independent
- Assumption 3: For any given x, the distribution of error is normal
- Assumption 4: The distribution of population errors for each x has the same (constant) standard deviation
Degrees of Freedom
The degrees of freedom for a simple linear regression model are,
Standard deviation of errors is calculated as
Where,
Total Sum of Squares (SST)
The total sum of squares, denoted by SST, is calculated as,
Regression Sum of Squares (SSR)
The regression sum of squares denoted by SSR is,
Coefficient of determination
The Coefficient of determination denoted by
and
The higher the value of r2, the more successful is simple linear regression model in explaining y variation
Multiple Linear Regression
Multiple linear regression: involves more than one predictor variable
- Training data is of the form (X1, y1), (X2, y2),…, (X|D|, y|D|)
- Ex. For 2-D data, we may have: y = w0 + w1 x1+ w2 x2
Views: 4